https://doi.org/10.1140/epjd/s10053-025-00966-3
Regular Article - Atomic Physics
On matrix elements of the vector physical quantities
Department of Applied Mathematics, University of Western Ontario, N6H 5B7, London, Ontario, Canada
Received:
27
November
2024
Accepted:
22
January
2025
Published online:
14
February
2025
Methods of angular momenta are modified and used to solve some actual problems in quantum mechanics. In particular, we re-derive some known formulas for analytical and numerical calculations of matrix elements of the vector physical quantities. These formulas are applied to a large number of quantum systems which have an explicit spherical symmetry. Multiple commutators of different powers of the angular momenta 
and vector-operator 
are determined in the general form. Calculations of the expectation values averaged over orbital angular momenta are also described in detail. This effective and elegant old technique, which was successfully used by Enrico Fermi and Aage Bohr, is almost forgotten in modern times. We also discuss quantum systems with additional relations (or constraints) between some vector-operators and orbital angular momentum. For similar systems such relations allow one to obtain some valuable additional information about their properties, including the bound state spectra, correct asymptotics of actual wave functions, etc. As an example of unsolved problems we consider applications of the algebras of angular momenta to investigation of the one-electron, two-center (Coulomb) problem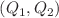 
. For this problem it is possible to obtain the closed analytical solutions which are written as the ‘correct’ linear combinations of products of the two one-electron wave functions of the hydrogen-like ions with the nuclear charges 
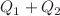and 
, respectively. However, in contrast with the usual hydrogen-like ions such hydrogenic wave functions must be constructed in three-dimensional pseudo-Euclidean space with the metric (
).
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, SIF and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
