https://doi.org/10.1140/epjd/s10053-024-00894-8
Regular Article - Quantum Information
Achieving quantum metrological performance and exact Heisenberg limit precision through superposition of s-spin coherent states
1
LPHE-Modeling and Simulation, Faculty of Sciences, Mohammed V University in Rabat, Rabat, Morocco
2
Centre of Physics and Mathematics, CPM, Faculty of Sciences, Mohammed V University in Rabat, Rabat, Morocco
3
Center of Excellence in Quantum and Intelligent Computing, Prince Sultan University, Riyadh, Saudi Arabia
Received:
22
March
2024
Accepted:
5
July
2024
Published online:
18
July
2024
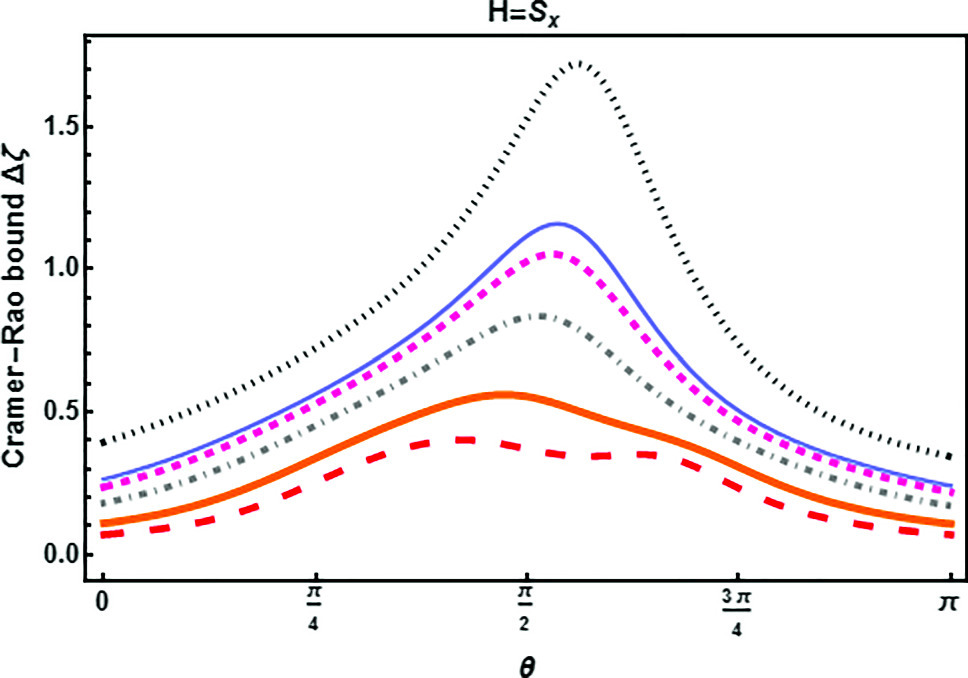
In quantum phase estimation, the Heisenberg limit provides the ultimate accuracy over quasi-classical estimation procedures. However, realizing this limit hinges upon both the detection strategy employed for output measurements and the characteristics of the input states. This study delves into quantum phase estimation using s-spin coherent states superposition. Initially, we delve into the explicit formulation of spin coherent states for a spin 
. Both the quantum Fisher information and the quantum Cramer–Rao bound are meticulously examined. We analytically show that the ultimate measurement precision of spin cat states approaches the Heisenberg limit, where uncertainty decreases inversely with the total particle number. Moreover, we investigate the phase sensitivity introduced through operators 
, 
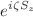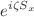and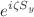 
, subsequently comparing the resultants findings. In closing, we provide a general analytical expression for the quantum Cramér–Rao bound applied to these three parameter-generating operators, utilizing general s-spin coherent states. We remarked that attaining Heisenberg-limit precision requires the careful adjustment of insightful information about the geometry of s-spin cat states on the Bloch sphere. Additionally, as the number of s-spin increases, the Heisenberg limit decreases, and this reduction is inversely proportional to the s-spin number.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, SIF and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
