https://doi.org/10.1140/epjd/s10053-023-00756-9
Regular Article - Nonlinear Dynamics
Soliton dynamics for generalized Chafee–Infante equation with power-law nonlinearity
School of Science, Jiangsu University of Science and Technology, 212100, Zhenjiang, China
Received:
4
May
2023
Accepted:
11
September
2023
Published online:
10
October
2023
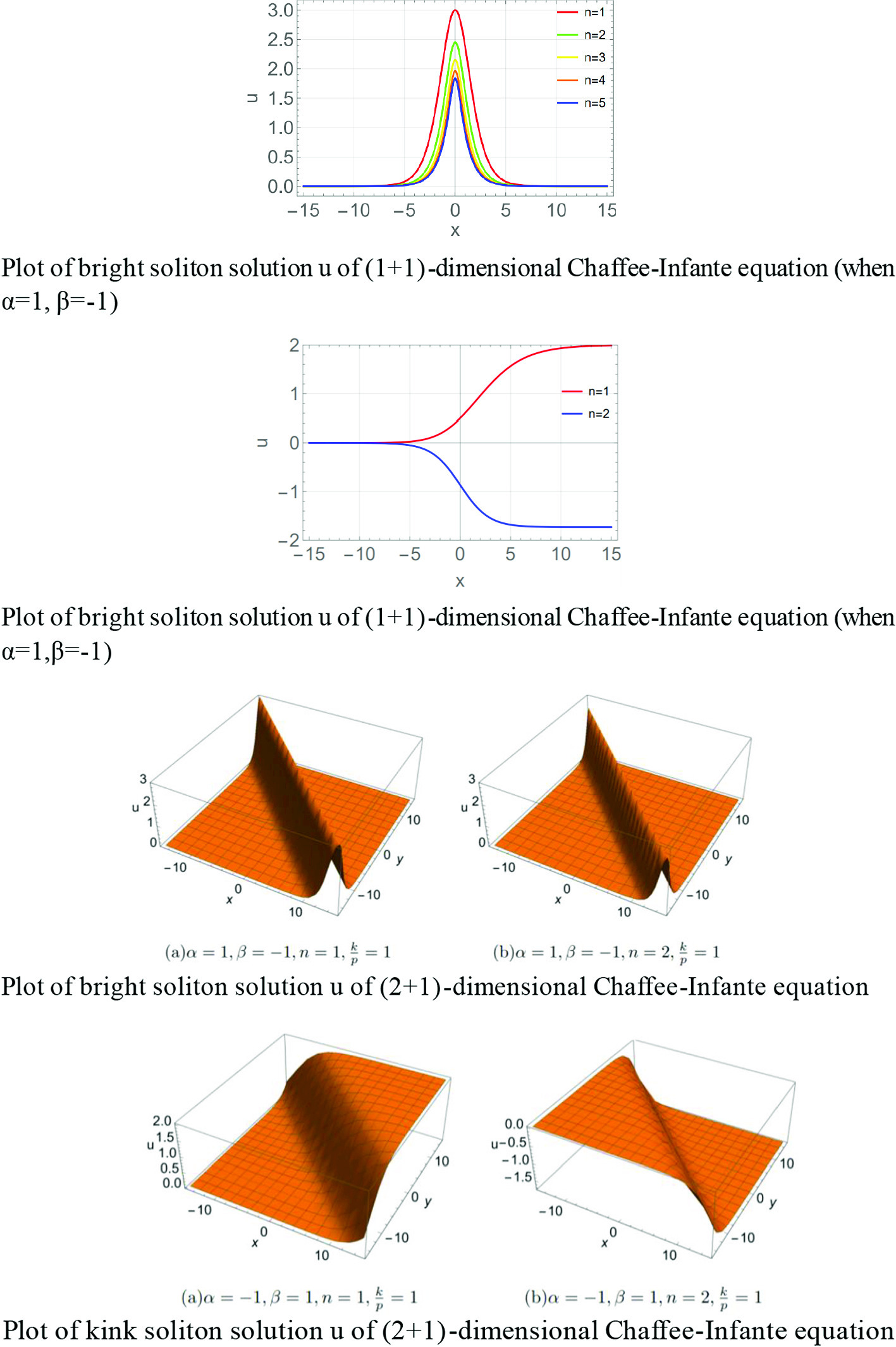
For systems modeled by the generalized Chafee–Infante equation with arbitrary nonlinear power index in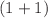 
-dimensional and 
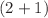-dimensional scenarios, we investigate the soliton dynamics utilizing the modified F-expansion method and novel ansatz of F-base function. We derived the bright soliton solution and kink soliton solution supported by the generalized Chafee–Infante equation system in both 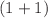- and 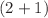-dimensional cases. We gave graphical illustrations of the derived soliton solutions in one and two dimensions and analyzed the stability of the bright soliton and kink soliton solutions in two-dimensional format. The theoretical results presented in this work can be used to guide the experimental observation of solitons in systems modeled by the generalized Chafee–Infante equation.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, SIF and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
