https://doi.org/10.1140/epjd/s10053-023-00703-8
Regular Article – Nonlinear Dynamics
Dynamics of exact solutions of nonlinear resonant Schrödinger equation utilizing conformable derivatives and stability analysis
Department of Mathematics, Faculty of Science, University of Gujrat, 50700, Gujrat, Pakistan
Received:
31
March
2023
Accepted:
14
June
2023
Published online:
28
June
2023
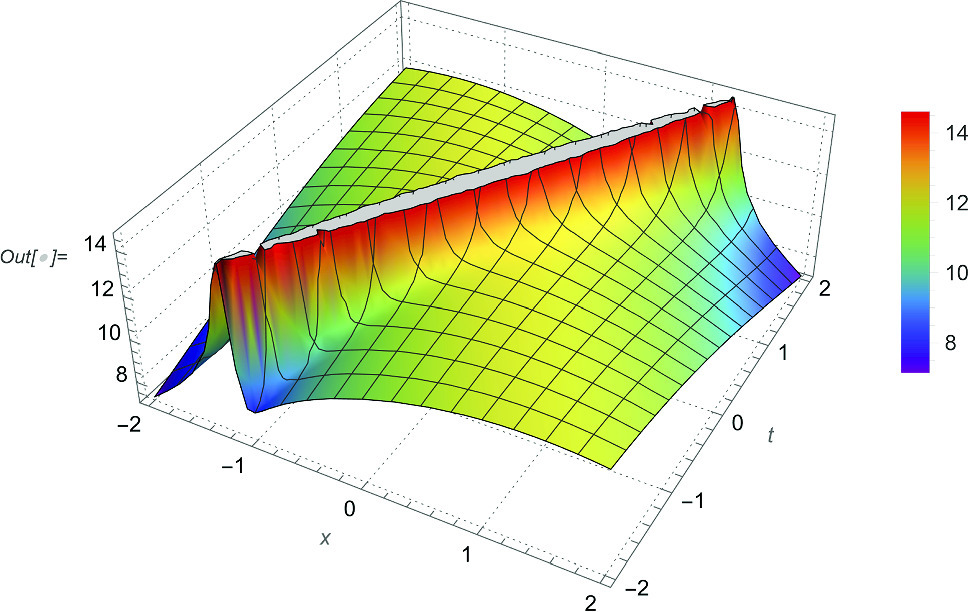
In this paper, we consider the conformable resonant nonlinear Schrödinger equation (CRNLSE) incorporating Kerr law nonlinearity and provide some new analytical solutions. Three analytical methods such as the Exp-function method, modified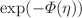 
-expansion function method, and 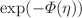-expansion function method are utilized to handle this problem. These methods yield various innovative and fascinating solutions, including trigonometric, exponential, periodic, bright, singular, dark, and rational solutions, as well as their constraint conditions. Moreover the modulation instability (MI) of the consider model is also investigated. For each solution discovered, 2D, 3D, and contour plots are also sketched to clarify their physical configuration. The reported solutions enhance the previously established results. The solutions demonstrate that these methods are efficient and effective for locating traveling wave solutions and could be a beneficial tool for handling other complex nonlinear partial differential equations (NLPDEs) emerge in diversified scientific fields such as hydrodynamics, nonlinear optics, nonlinear fibers and plasmas.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, SIF and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
