https://doi.org/10.1140/epjd/e2003-00225-3
Modular construction of special mixed quantum states
Institute of Theoretical Physics I, University of Stuttgart, Pfaffenwaldring 57, 70550 Stuttgart, Germany
Corresponding author: a mathias@theo1.physik.uni-stuttgart.de
Received:
3
December
2002
Revised:
3
March
2003
Published online:
29
July
2003
For a homogeneous quantum network of N subsystems with n levels each we consider separable generalized Werner states.
A generalized Werner state is defined as a mixture of the totally mixed state and an arbitrary pure state 
:
with a mixture coefficient ϵ.
For this density operator 
to be separable, ϵ will have an
upper bound 
.
Below this bound one should alternatively be able to reproduce by
a mixture of entirely separable input-states. For this purpose we introduce a
set of modules, each contributing elementary coherence properties with respect to a generalized coherence vector. Based on
these there exists a general step-by-step mixing process for any
.
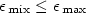For being a cat-state it is possible to define an optimal
process, which produces
states right up to the separability boundary (
).
PACS: 03.65.Ud – Entanglement and quantum nonlocality (e.g. EPR paradox, Bell's inequalities, GHZ states, etc.) / 03.67.-a – Quantum information / 03.65.-w – Quantum mechanics
© EDP Sciences, Società Italiana di Fisica, Springer-Verlag, 2003
