https://doi.org/10.1007/s100530050539
Reconstruction of systems with delayed feedback: II. Application
1
Istituto Nazionale di Ottica Applicata, Largo E. Fermi 6,
50125 Firenze, Italy
2
Max-Planck-Institut für Physik komplexer Systeme,
Nöthnitzer Str. 38, 01187 Dresden, Germany
3
INFM, Unità di Firenze, 50125 Firenze, Italy
Received:
17
December
1999
Published online: 15 May 2000
We apply a recently proposed method for the analysis of time series
from systems with delayed feedback to experimental data generated by a
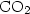laser. The method allows estimating the delay time
with an error of the order of the sampling interval, while an approach
based on the peaks of either the autocorrelation function, or the time
delayed mutual information would yield systematically larger values.
We reconstruct rather accurately the equations of motion and, in turn, estimate
the Lyapunov spectrum even for high dimensional attractors.
By comparing models constructed for different "embedding dimensions"with
the original data, we are able to find the minimal faithful model.
For short delays, the results of our procedure have been cross-checked
using a conventional Takens time-delay embedding. For large
delays, the standard analysis is inapplicable since the dynamics becomes
hyperchaotic. In such a regime we provide the first experimental evidence
that the Lyapunov spectrum, rescaled according to the delay time, is
independent of the delay time itself. This is in full analogy with the
independence of the system size found in spatially extended systems.
PACS: 02.30.Ks – Delay and functional equations / 05.45.Tp – Time series analysis
© EDP Sciences, Società Italiana di Fisica, Springer-Verlag, 2000
