https://doi.org/10.1007/s10053-000-8800-6
The open path phase for degenerate and non-degenerate systems and its relation to the wave-function modulus
1
Department of Physics and Applied Mathematics,
Soreq NRC, Yavne 81800, Israel
2
Research Institute,
College of Judea and Samaria, Ariel 44284, Israel
3
Faculty of Engineering,
Tel-Aviv University, Tel-Aviv 69978, Israel
Received:
16
May
1999
Published online: 13 August 2013
We calculate the open path phase in a two state model with a slowly (nearly adiabatically)
varying time-periodic Hamiltonian and trace its continuous development during a period.
We show that the topological (Berry) phase attains π or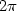 
depending on whether there is or
is not a degeneracy in the part of the parameter space enclosed by the trajectory.
Oscillations are found in the phase. As adiabaticity is approached, these become both more frequent and less pronounced and the phase jump becomes increasingly more steep.
Integral relations between the phase and the amplitude modulus (having the form of
Kramers-Kronig relations, but in the time domain) are used as an alternative way to
calculate open path phases. These relations attest to the observable nature of the
open path phase.
PACS: 03.65.Bz – Foundations, theory of measurement, miscellaneous theories (including Aharonov-Bohm effect, Bell inequalities, Berry's phase) / 03.65.Ge – Solutions of wave equations: bound states
© EDP Sciences, Società Italiana di Fisica, Springer-Verlag, 2000
